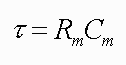3.1 Changes in the Spatial Distribution of Charge
| Video of lecture |
Once an action potential is initiated at one point in the nerve cell, how does it propagate to the synaptic terminal region in an all-or-nothing fashion?
Figure 3.1 shows a schematic diagram of an axon and the charge distributions that would be expected to occur along the membrane of that axon. Positive charges exist on the outside of the axon and negative charges on the inside. Now consider the consequences of delivering some stimulus to a point in the middle of the axon. If the depolarization is sufficiently large, voltage-dependent sodium channels will be opened, and an action potential will be initiated.
Figure 3.1 |
Consider for the moment "freezing" the action potential at its peak value. Its peak value now will be about +40 mV inside with respect to the outside. Unlike charges attract, so the positive charge will move to the adjacent region of the membrane. As the charge moves to the adjacent region of the membrane, the adjacent region of the membrane will depolarize. If it depolarizes sufficiently, as it will, voltage-dependent sodium channels in the adjacent region of the membrane will be opened and a "new" action potential will be initiated. This charge distribution will then spread to the next region and initiate other "new" action potentials. One way of viewing this process is with a thermal analogue. You can think of an axon as a piece of wire coated with gunpowder (the gunpowder is analogous to the sodium channels). If a sufficient stimulus (heat) is delivered to the wire, the gunpowder will ignite, generate heat, and the heat will spread along the wire to adjacent regions and cause the gunpowder in the adjacent regions to ignite.
3.2 Determinants of Propagation Velocity
A great variability is found in the velocity of the propagation of action potentials. In fact, the propagation velocity of the action potentials in nerves can vary from 100 meters per second (580 miles per hour) to less than a tenth of a meter per second (0.22 miles per hour). Why do some axons propagate information very rapidly and others slowly? In order to understand how this process works, it is necessary to consider two so-called passive properties of membranes, the time constant and the space or length constant. Why are these called passive properties? They have nothing to do with any of the voltage-dependent conductances discussed earlier. They have nothing to do with any pumps or exchangers. They are intrinsic properties of all biological membranes.
|
Figure 3.2 |
Time Constant. First, consider a thermal analogue. Place a block of metal at 10oC on a hotplate at 100oC. How would the temperature change? It will increase from its initial value of 10oC to a final value of 100oC. But the temperature will not change instantly. In fact, it would change as an exponential function of time. An analogous situation occurs in nerve cells, when they receive an instantaneous stimulus. The figure at right represents an idealized nerve cell. The recording electrode initially measures a potential of -60 mV (the resting potential). At some point in time (time 0), the switch is closed. The switch closure occurs instantaneously and as a result of the instantaneous closure, instantaneous current flows through the circuit. (This is equivalent to slamming the block of metal on the hotplate.) Note that despite the fact that this stimulus changes instantly, the change in potential does not occur instantaneously. It takes time for the potential to change from its initial value of -60 mV to its final value of -50 mV. There is a total of 10 mV depolarization, but the change occurs as an exponential function of time.
There is a convenient index of how rapidly exponential functions change with time. The index is denoted by the symbol τ and called the time constant. It is defined as the amount of time it takes for the change in potential to reach 63% of its final value. (Why 63%?) In this example, the potential changes from -60 to -50 and the 63% value is -53.7 mV. Thus, the time constant is 10 msec. The smaller the time constant, the more rapid will be the change in response to a stimulus. Therefore, if this neuron had a time constant of 5 msec, then in 5 msec the membrane potential would reach -53.7 mV. The time constant is analogous to the 0 to 60 rating of a high performance car; the lower the 0 to 60 rating, the faster the car. The lower the time constant, the faster or more rapidly a membrane will respond to a stimulus. The effects of the time constant on propagation velocity will become clear below.
The time constant is a function of two properties of membranes, the membrane resistance (Rm ) and the membrane capacitance (Cm ). Rm is the inverse of the permeability; the higher the permeability, the lower the resistance, and vice versa. Membranes, like the physical devices known as capacitors, can store charge. When a stimulus is delivered, it takes time to charge up the membrane to its new value.
|
[Please consult a college-level textbook on physics for a review of the basic properties of resistors and capacitors. For an additional review of resistors, capacitors and time constants and the use of hydraulic analogues to understand them see: Byrne, J. H., Understanding Electricity with Water, epub, Lulu.com, 2011.]
Space Constant. Consider another thermal analogue. Take a long, metal rod that is again initially at 10oC and consider the consequences of touching one end of the rod to a hotplate which is at 100oC. (Assume that it is placed there for a certain amount of time to allow the temperature changes to stabilize.) How would the temperature be distributed along the length of the rod? There would be a temperature gradient along the rod because of the increasing loss of heat with greater distances from the heat source. The temperature gradient can be described by an exponential function of distance because of the physical processes involved.
|
Figure 3.3 |
An analogous situation occurs in nerve cells. The figure at left represents an idealized nerve cell in which recordings are made from different regions along the axon at 1 mm increments. The cell body is impaled with a stimulating electrode connected to a battery, the value of which changes the potential of the cell body to -50 mV (the equivalent of putting a 10oC rod on a 100oC hot plate). This axon, even though it initially had a spatially uniform resting potential of -60 mV, now has a potential of -50 mV in the soma because that is the region in which the stimulus is applied. However, the potential is not -50 mV all along the axon; it varies as a function of distance from the soma. One mm away the potential is -56 mV; at 2 mm away it is even closer to -60 mV; and far enough along the axon, the potential of the axon is -60 mV, the resting potential. Just as there is an index for how a change in potential changes with the time (the time constant), there is also an index denoted by the symbol λ (called the space constant or the length constant) which is an indication of how far a potential will spread along an axon in response to a subthreshold stimulus at another point. In Figure 3.3, the space constant or length constant is 1 mm. In 1 mm the potential will change by 63% of its final value. If λ was greater than 1 mm, the potential would spread a greater distance. If λ was 1/2 mm, the potential would spread less along the axon. Thus, whereas the time constant is an index of how rapidly a membrane would respond to a stimulus in time, the space constant is an index of how well a subthreshold potential will spread along an axon as a function of distance. The space constant is a passive property of membranes. Although it influences the rate of propagation of the action potentials, it is an independent process. It is like the surface of a race track and the action potential is like the race car. If the surface is muddy, the car will go slow, if it is firm and paved, the same car will be able to go much faster.
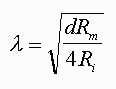 |
The length constant can be described in terms of the physical parameters of the axon, where d is the diameter of the axon, Rm is, as before, the membrane resistance, the inverse of the permeability, and Ri is the internal resistance (resistance of the axoplasm). Ri is an indicator of the ability of charges to move along the inner surface of the axon. A small subthreshold change in the charge distribution at one point along an axon will spread along the axon, but as it does some will diffuse back out of the membrane and some will continue to move along the axon. If the resistance of the membrane (Rm) is high, less will leak out and relatively more will move along the axon. Increasing Rm is like putting insulation on a metal rod and heating the rod at one end. With more insulation (more resistance to heat loss to the outside of the rod), more heat will travel along the inside of the rod.
Propagation Velocity. How are the time constant and the space constant related to propagation velocity of action potentials? The smaller the time constant, the more rapidly a depolarization will affect the adjacent region. If a depolarization more rapidly affects an adjacent region, it will bring the adjacent region to threshold sooner. Therefore, the smaller the time constant, the more rapid will be the propagation velocity. If the space constant is large, a potential change at one point would spread a greater distance along the axon and bring distance regions to threshold sooner. Therefore, the greater the space constant, the more rapidly distant regions will be brought to threshold and the more rapid will be the propagation velocity. Thus, the propagation velocity is directly proportional to the space constant and inversely proportional to the time constant. There are separate equations that describe both the time constant and the space constant. The insight above allows us to make a new equation that combines the two.
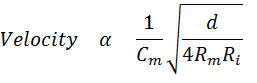 |
The equation provides insights into how it is possible for different axons to have different propagation velocities. One way of endowing an axon with a high propagation velocity is to increase the diameter. However, there is one serious problem in changing the propagation velocity by simply changing the diameter. To double the velocity, it is necessary to quadruple the diameter. Clearly there must be a better way of increasing propagation velocity than by simply increasing the diameter.
Another way to increase the propagation velocity is to decrease the membrane capacitance. This can be achieved by coating axons with a thick insulating sheath known as myelin. One potential problem with this approach is that the process of covering the axon would cover voltage-dependent Na+ channels. If Na+ channels are occluded, it would be impossible to generate an action potential. Instead of coating the entire axon with the myelin, only sections are coated and some regions called nodes are left bare.
3.3 Propagation in Myelinated Fibers
|
Figure 3.4 |
Propagation of action potentials in myelinated fibers is illustrated in Figure 3.4. Start with an action potential at a node on the left. In the absence of myelin, the action potential would propagate actively through the simple mechanisms discussed above. However, now the myelin occludes all the voltage-dependent sodium channels so the action potential can not propagate actively. (In fact, myelinated axons do not even have sodium channels in the internodal region.) Rather, the potential change produced by the action potential at one node spreads in the internodal region along the axon passively just as the temperature would spread along a long metal rod. The potential spreads, but gets smaller (decrements), just as a temperature change induced at one end of a rod would get smaller as it spreads along a rod.
Now consider the point at which the passively spreading potential reaches the next node. A "new" action potential will be initiated. The stimulus for this action potential is the depolarization that emerges from the end of the myelin. Each node acts as a "relay station" that renews the decremented signal. Think of the gunpowder analogue again, but this time coat the rod with some insulation and put gunpowder only at the bare regions. Because of the insulation, a temperature change produced by the ignition of the gunpowder will spread effectively along the metal rod. Some loss of temperature will occur but it will be sufficient to ignite the gunpowder at the next region and the process will repeat itself.